
Pictet: Modifizierung der Taylor-Regel für genauere Prognosen der Zinssätze
Wie sich die Zinssätze in diesem Jahr wohl entwickeln werden? Wir haben eine abgewandelte Version der Taylor-Regel entwickelt, die Antworten liefern könnte.
17.04.2024 | 07:00 Uhr
Die Geldpolitik hat grossen Einfluss auf die Anlagerenditen – egal in welcher Anlageklasse. Die Vorhersage der Leitzinsentwicklung ist jedoch alles andere als leicht. Das gilt insbesondere jetzt, da die Debatte darüber geführt wird, wie schnell und wie stark die USA und die Eurozone die Zinssätze senken werden, wenn die Inflation nachlässt.
Ein nützliches Instrument zur Schätzung der Zinssatzentwicklung ist die Taylor-Regel. Es gibt sie schon seit etlichen Jahrzehnten, aber sie ist immer noch eines der nützlichsten Modelle, an dem sich die Zentralbanken für ihren geldpolitischen Kurs orientieren, wenn ihre Glaubwürdigkeit auf dem Spiel steht. Ihre grösste Stärke ist, dass sie so einfach ist. Der Regel zufolge sollten die nominalen Leitzinsen in der Nähe der Wachstumsrate des nominalen BIP liegen, zuzüglich oder abzüglich eines Koeffizienten, der misst, wie weit die Inflation vom Ziel der Zentralbank entfernt ist und wie sich das Wachstum im Vergleich zu seinem langfristigen Trend entwickelt.
Gerade weil die Regel so einfach ist, stösst sie schnell an ihre Grenzen. Nicht zuletzt, weil die Zentralbanken neben Wachstum und Inflation noch viele andere Faktoren berücksichtigen. Wir haben daher unsere eigene, modifizierte Version der Taylor-Regel entwickelt, die unserer Meinung nach der Realität besser Rechnung trägt.
Unser Modell deutet darauf hin, dass Zinssenkungen in den USA und im Euroraum in diesem Jahr geringer ausfallen werden als von der traditionellen Taylor-Regel vorhergesagt – wenn auch stärker als derzeit von den Finanzmärkten eingepreist.1 Es lässt auch auf eine eher mässige Straffung durch die Bank of Japan schliessen, die kürzlich ihre Negativzinspolitik aufgegeben hat.

Die US-Wirtschaft befindet sich jetzt im letzten Abschnitt ihrer Expansionsphase, und es wird erwartet, dass sich die Wirtschaftstätigkeit im weiteren Verlauf des Jahres deutlich abkühlt. Das deutet auf Zinssenkungen hin. Entscheidend ist jedoch, dass der Abschwung in den USA nicht schwerwiegend genug ist, um die US-Notenbank zu einer aggressiven Lockerung zu veranlassen, insbesondere solange die Inflation stabil bleibt und der Arbeitsmarkt stark ist. Vor diesem Hintergrund zeigt unser Modell, dass der Zielzinssatz der Fed bis Ende 2024 auf 4,3% gesenkt werden könnte, was einer potenziellen Lockerung von rund 100 Basispunkten entspricht. Diese Zinsschritte sind geringer als von der traditionellen Taylor-Regel vorhersagt, sie übersteigen aber die von den Finanzmärkten eingepreisten 60 Basispunkte.
Auch aus Sicht der Europäischen Zentralbank liegt die Inflation immer noch in einem Bereich, der in der Vergangenheit Anlass zur Sorge gab. Unsere Untersuchungen zeigen, dass dies eine Lockerung auf den Plan rufen könnte, die moderater ausfallen dürfte als durch die traditionelle Taylor-Regel vorgegeben. Der Einlagensatz wird am Jahresende wahrscheinlich bei 2,3% liegen (aktuell sind es 4%). Wie auch bei den USA schätzen die Märkte den Spielraum für Zinssenkungen möglicherweise zu niedrig ein, wobei die aktuellen Werte darauf hindeuten, dass die Zinssätze Ende 2024 knapp über 3% liegen werden.
Für Japan geht unser Modell davon aus, dass die Bank of Japan die Zinssätze bis Jahresende auf 0,3% anheben könnte. Wechselkursüberlegungen – bzw. genauer gesagt die Möglichkeit, dass Zinserhöhungen einen starken Anstieg des japanischen Yen auslösen – werden wahrscheinlich eine aggressivere Straffung verhindern.
Die Schweiz hingegen stellt eine Ausnahme dar. Sowohl die traditionelle Taylor-Regel als auch unsere modifizierte Version legen nahe, dass die Zinssätze höher sein dürften als jetzt und dass die jüngste Senkung des Leitzinses, einhergehend mit niedrigeren Kreditkosten, nicht gerechtfertigt war, da die Schweizerische Nationalbank ihren geldpolitischen Normalisierungsprozess im Jahr 2023 nicht wirklich abgeschlossen hat. Die SNB verwies darauf, dass die jüngsten geldpolitischen Entscheidungen unter dem Gesichtspunkt des Risikomanagements getroffen wurden – in diesem Fall wurde das Risiko, die Zinssätze nicht zu senken und möglicherweise eine weitere Aufwertung des Schweizer Frankens zuzulassen, als das schwerwiegendere eingestuft. Diese Diskrepanz zwischen der tatsächlichen Geldpolitik und unserem Modell könnte eine neue Ära für den Kurs der SNB markieren, da die Beziehung zwischen den beiden Faktoren in den vergangenen Jahren relativ eng war.
Hauptaugenmerk auf dem Modell
Wie aber sind wir zu unseren Schlussfolgerungen gelangt?
Wir haben damit begonnen, nach Möglichkeiten zu suchen, wie man dem Umstand Rechnung tragen kann, dass die traditionelle Taylor-Regel ein lineares Modell ist, die Zentralbankpolitik aber nicht. Das Ausmass der Zinsreaktion auf eine Veränderung der nominalen Wachstumsrate um 50 Basispunkte wird also je nach tatsächlicher Höhe des Wachstums unterschiedlich ausfallen. So zeigt unsere Analyse, dass die Fed tendenziell aggressiver reagiert, wenn das BIP-Wachstum über dem Potenzial liegt und Zinserhöhungen erforderlich sind, als wenn es unter dem Potenzial liegt und Zinssenkungen gefordert sind. Und neben Wachstum und Inflation gibt es noch andere Faktoren zu berücksichtigen. Nehmen wir die Nachwirkungen der Covid-Pandemie. Nach der Taylor-Regel hätte die Fed im Jahr 2021 mit der schrittweisen Anhebung der Zinssätze beginnen sollen. Stattdessen erhöhte die US-Notenbank angesichts der Unsicherheit über die wirtschaftliche Erholung nach der Pandemie erst im März 2022 die Zinssätze, nachdem die Folgen des Ukraine-Kriegs zu einem Inflationsschub geführt hatten.
Dies zeigt, dass keine zwei Situationen gleich sind, unabhängig von den zugrunde liegenden wirtschaftlichen Fundamentaldaten, die jedes Mal eine andere geldpolitische Reaktion hervorrufen könnten.
Darüber hinaus beinhalten Prognosen für künftiges Wachstum und Inflation in der Regel eine Reihe von Wahrscheinlichkeiten und nicht einen einzelnen endgültigen Wert oder Parameter.
Dann gibt es noch die Wechselkurse, die in engem Zusammenhang mit der Inflation und demzufolge mit der Zentralbankpolitik stehen. In den USA schlägt das weniger zu Buche, da es sich um eine grosse, relativ geschlossene Volkswirtschaft handelt, die nicht sehr empfindlich auf Wechselkursschwankungen reagiert. Für die EZB ist das jedoch ein wichtiger Faktor – in der Vergangenheit tendierte sie zu aggressiven Zinssenkungen, wenn der Euro inflationsbereinigt um mehr als 2,5% aufwertete.
Die traditionelle Taylor-Regel ist eine „rudimentäre“ Formel, die diese komplexen Elemente nicht berücksichtigt. Wir glauben, dass ihre Ergebnisse genauer wären, wenn sie das täte.
Unsere modifizierte Version der Taylor-Regel folgt daher einem nichtlinearen, semiparametrischen Ansatz, der Währungsschwankungen und die wechselseitige Interaktion zwischen Wechselkursen und Inflation einbezieht.
Für Japan nahmen wir eine Variable in das Modell auf, die der Bedeutung der Anleihekäufe für die Geldpolitik Rechnung trägt. Wir berücksichtigten dazu das Wachstum der M4-Geldmenge, das zeigt, inwieweit sich die Anleihekäufe in der breiteren Wirtschaft niederschlagen. In der Vergangenheit reagierte die Bank of Japan auf eine hohe Inflation deutlich aggressiver als auf eine niedrige. Ausserdem tendierte sie dazu, ein starkes M4-Wachstum durch eine Straffung der Geldpolitik auszugleichen.
Nachdem wir unser Modell auf der Grundlage von Daten aus den späten 1980er Jahren (je nach betrachtetem Land) erstellt hatten, führten wir einen Backtest für den Zeitraum von Ende 2014 bis 2019 durch, wobei wir uns die darauffolgenden vier Quartale anschauten, um zu sehen, wie effektiv es war (ein sogenannter „Out-of-Sample“-Test). Unsere Analyse zeigte, dass die modifizierte Taylor-Regel die Geldpolitik im Durchschnitt genauer vorhersagte als das ursprüngliche lineare Modell und einen geringeren Standardschätzfehler (Root Mean Squared Error, RMSE) aufwies. Dies galt für die USA, die Eurozone, Japan und die Schweiz (siehe Abbildung). Auch die Fehlerquote war mit einem Wert unter 1,2 für alle vier Länder erfreulich gering.
Abb. 2 – Weniger FehlerRMSE für Out-of-Sample-Tests unseres modifizierten Taylor-Regel-Modells
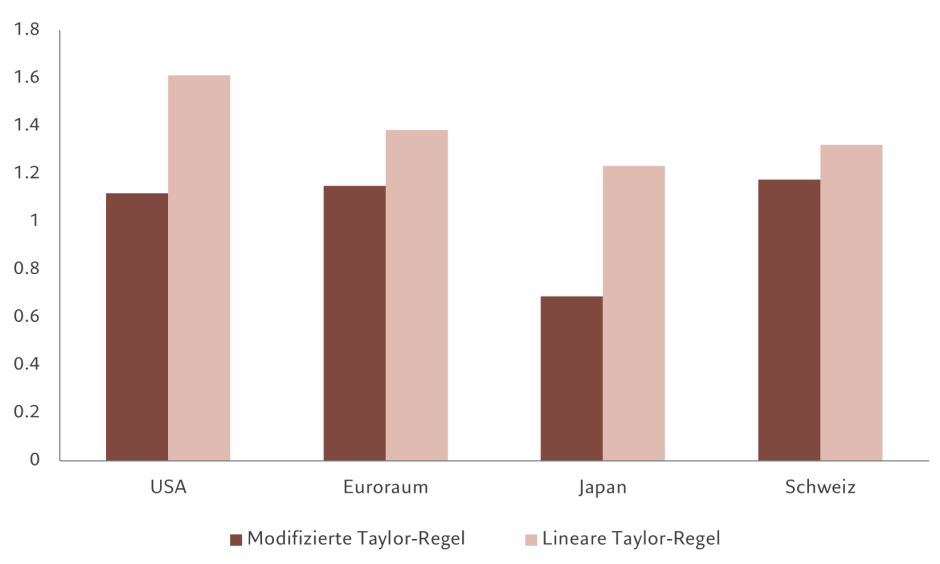
Quellen: Pictet Asset Management, Refinitiv & CEIC. Daten beziehen sich auf den Zeitraum 01.01.2014–31.12.2019.
Nach einer Analyse der Daten der letzten 30 Jahre kommen wir zu dem Ergebnis, dass ein nichtlineares und semiparametrisches Taylor-Regel-Setup2 für die grossen Zentralbanken der Industrie- und Schwellenländer am besten geeignet ist, weil es die Interaktion zwischen Inflation und Wechselkurs sowie im Falle Japans zusätzlich den Faktor des Wachstums der M4-Geldmenge berücksichtigt.
Darüber hinaus zeigt unsere statistische Out-of-Sample-Analyse, dass ein solches Modell in den meisten Fällen eine genauere Vorhersage der nächsten Zinsentscheidungen der Zentralbanken in einem Echtzeit-Datenumfeld ermöglicht als die traditionelle lineare, parametrische Taylor-Regel.
Für das kommende Jahr deutet unser Modell auf weniger aggressive Zinssenkungen in den USA und Europa hin. Gegenüber der ursprünglichen Regel spiegeln sich darin ein vorsichtigeres Verhalten der Zentralbanken und ein gemässigteres Zinsanhebungstempo in Japan wider. Die wichtigste Erkenntnis für Investoren ist jedoch, dass die Zinssenkungen in den USA und Europa selbst unter Berücksichtigung des komplexen Verhaltens der Zentralbanken wahrscheinlich umfassender ausfallen werden als von den Märkten derzeit eingepreist. Diese zusätzliche Dimension kann den Bewertungen und Investmententscheidungen zugrunde gelegt werden.
[1] Marktpreise vom 08.04.2024.
[2] Ein semiparametrisches Modell ist ein statistisches Modell, das sowohl parametrische als auch nichtparametrische Komponenten enthält (bei denen wir glatte Funktionen der Variablen anstelle von Parametern schätzen).




Diesen Beitrag teilen: